Careful, intentional, and mindful questioning is one of the most powerful tools a skillful teacher possesses (Costa & Kallick, 2000). Teachers can use open-ended questions during math instruction or assessments to learn how students are problem-solving.
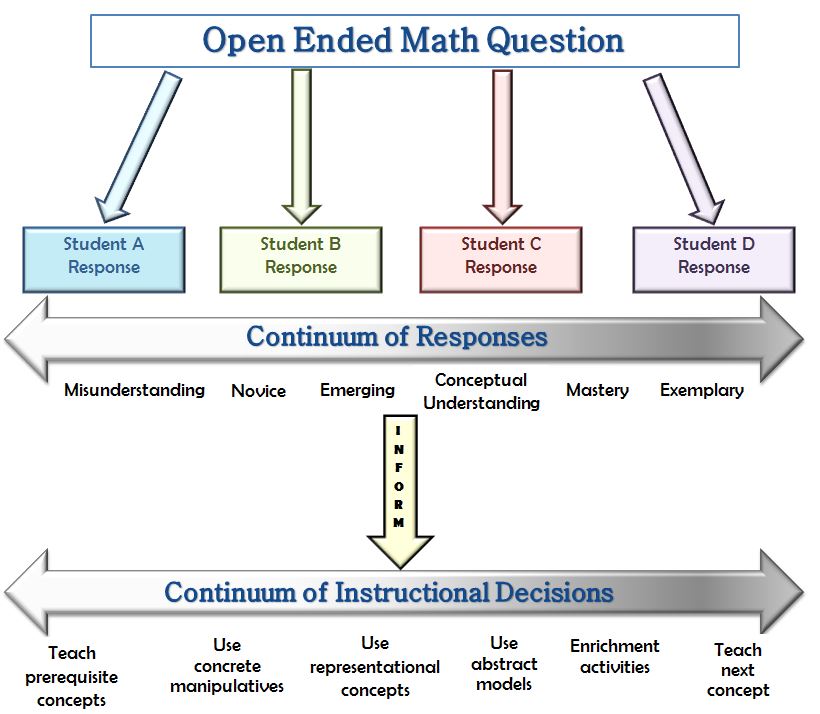
A question is considered open-ended when it is framed in such a way that a variety of responses or approaches are possible (Small, 2009). As shown in Figure 1, open-ended math questions are designed to uncover student understanding and misunderstandings. The responses are used to inform instruction rather than to make evaluative decisions (Rose & Arline, 2009).
Teachers analyze students’ responses to questions in order to learn how they think. The responses reveal what students know and how they apply that knowledge. Teachers then use this information to design instruction that supports student learning. Additionally, open-ended questions provide opportunities for students to respond and contribute at their respective levels. This is especially important for struggling students, since they are likely to be passive learners (Lovin, Kyger, & Allsopp, 2004).
Figure 1 illustrates how asking an open-ended question identifies students’ understanding along a continuum. Teachers use this information to determine where to begin new instruction.
Figure 1. Continuum of student responses and instructional decisions.
The examples below from Instructional Consultation and Assessment Team (ICAT) Manual Book 3 (Gravois, Gickling, & Rosenfield, 2011, pp. 82-84) illustrates examples of open-ended questions what the responses reveal about students’ understanding of a variety of math concepts.
Specific Assessment: Mathematical Thinking
Good Math Questions Share the Following Features
- Begin with what the student knows
- Engage students in the math skills and thinking that you are trying to assess
- Require more than facts to resolve
- Are open-ended and have more than one answer
Consider the following types of mathematical open-ended questions:
Number Sense
- Jack has 12 pets. Some are dogs and some are cats. How many dogs could Jack have, and how many cats could Jack have?
This question can show you:- Can the student count 12 items?
- Does the student know how to begin?
- Does the student start with 12 and count back, or does she start with a number and add on to 12? (i.e. 10 or 5)
- Does the student need counters or can he solve it mentally?
- Does the student demonstrate knowledge of an operational algorithm?
- I made a two-color tower with 6 blocks. What might my tower look like?
This question can show you:- What factors of 6 does the student use?
- Does the student know how to begin the problem?
- Does the student use counters or can she solve the problem mentally?
- Does the student demonstrate knowledge of an operational algorithm?
[showhide type=”post2″ more_text=”Addition and Subtraction Examples… show more” less_text=”Addition and Subtraction Examples… show less”]
- Lauren had 8 stickers. She shared some with Deb. How many stickers could Lauren have shared with Deb, and how many stickers could she have left?
- How does the student approach the problem?
- Does the student understand that something is being given away?
- Can the student count to 8?
- Does the student need manipulatives?[/showhide]
[showhide type=”post3″ more_text=”Multiplication Examples… show more” less_text=”Multiplication Examples… show less”]
- Suppose I wanted to find out the number of legs in the classroom? How could I do that?
- How does the student approach the problem?
- Does the student add each leg?
- Did the student multiply a number or group of number by 2?
- Does the student need manipulatives?[/showhide]
[showhide type=”post4″ more_text=”Division Examples… show more” less_text=”Division Examples… show less”]
- Joey is having some kids over for cupcakes. How many cupcakes will Joey have, and how many plates will he need if 5 cupcakes fit on a plate?
- How does the student approach the problem?
- Does the student use flexible strategies to solve and organize the problem?
- Does the student understand division?
- Does the student recognize the different steps involved in the problem?
- Does the student draw a picture or use manipulatives?[/showhide]
[showhide type=”post5″ more_text=”Fraction Examples… show more” less_text=”Fraction Examples… show less”]
- ¼ of the class is wearing yellow. What might a drawing of this look like?
- How does the student approach the problem?
- Does the student understand ¼?
- Does the student choose a set easily divided by ¼?
- Does the student understand parts of a set as opposed to parts of a whole?[/showhide]
[showhide type=”post6″ more_text=”Probability Examples… show more” less_text=”Probability Examples… show less”]
- Gloria had some marbles in a bag. Some were blue and some were red. It is more likely that you will pick red than blue. Draw a picture of what the marbles in the bag might look like.
- How does the student approach the problem?
- Does the student know what likely means?
- Does the student see the problem as a fraction, percent, or ratio?[/showhide]
[showhide type=”post7″ more_text=”Algebra Examples… show more” less_text=”Algebra Examples… show less”]
- Jacob wrote this statement on his homework paper:
8 + 6 = 7 + 3 + 4
Is this statement true? How do you know?
-
- Does the student work from right to left?
- Does the student see the equal sign as meaning the same, or does he see it as an action?
- Does the student add mentally or use another strategy to add the numbers?[/showhide]
[showhide type=”post8″ more_text=”Measurement Examples… show more” less_text=”Measurement Examples… show less”]
- A farmer had 36 yards of wood to build a fence around his new garden. Draw a sketch of what the garden might look like if the farmer uses all the wood.
- How does the student approach the problem?
- Does the student recognize and understand perimeter?
- Does the student use a number of sides that represents a multiple of 36?[/showhide]
[showhide type=”post9″ more_text=”Geometry Examples… show more” less_text=”Geometry Examples… show less”]
- Your teacher asks you to cut triangles out of a square. How many triangles might you cut? Draw a diagram and explain your answer.
- Does the student recognize a shape within shapes?
- Does the student recognize that the triangles keep repeating?
- Can the student explain how he found the triangles?
- I want to rearrange the 4 tables in the back of my room so that they are parallel with each other. Draw a sketch of what that might look like.
- How does the student approach the problem?
- Does the student understand parallel?
- Can the student make more than two items parallel?[/showhide]
[showhide type=”post10″ more_text=”Data Analysis Examples… show more” less_text=”Data Analysis Examples… show less”]
- Make a graph that represents how many people are in your house from 1:00AM until 9:00PM.
- How does the student approach the problem?
- What type of graph does the student use to display this data?
- How does the student interpret the data on the graph?
- Does the student understand time as intervals?
- Does the student understand that the data changes over time?
- Katie had a plant that was growing very slowly on a window sill that got no sunlight. She moved it to a sunny window. Then it started growing more quickly. Draw a graph that represents this story.
- How does the student approach the problem?
- What type of graph does the student use to display this data?
- How does the student interpret the data on the graph?
- Amy’s plant was growing quickly for a while. Then she forgot to water it for several days. That made it grow slowly. Draw a graph that represents this story.
- What type of graph does the student use to display this data?
- How does the student approach the problem?
- How does the student interpret the data on the graph?[/showhide]
[youtube]https://www.youtube.com/watch?v=_ofQ_WnQiZ4[/youtube]
(Burn, 1993a)
[youtube]https://www.youtube.com/watch?v=1puQxclB2aw#t=10[/youtube]
(Burn, 1993b)
Note to Readers: Please share how you are using open-ended questions in your classes or ask a question related to this topic by posting a comment at the end of this article.
References
Burn. M. (1993a). Mathematics: Assessing, understanding Cena. Retrieved from https://www.youtube.com/watch?v=_ofQ_WnQiZ4
Burn, M. (1993b). Mathematics: Assessing, understanding Jonathan. Retrieved from https://www.youtube.com/watch?v=1puQxclB2aw#t=10
Costa, A. L., & Kallick, B. (Eds.). (2000). Activating and engaging habits of mind. Alexandria, VA: Association for Supervision and Curriculum Development.
Gravois, T., Gickling, E., & Rosenfield, S. (2011). ICAT manual book 3. Baltimore, MD: ICAT Publishing.
Lovin, A., Kyger, M., & Allsopp, D. (2004). Differentiation for special needs learners. Teaching Children Mathematics, 11, 158-167.
Rose, C., & Arline, C. (2009). Uncovering student thinking in mathematics, Grades 6-12. Thousand Oaks, CA: Corwin Press.
Small, M., (2009). Good questions: Great ways to differentiate mathematics instruction. New York, NY: Teachers College Press.
| The following resources are available for check out from the T/TAC William & Mary Library |
|
 |
Good Questions for Math Teaching: Why Ask Them and What to Ask – Grades 5-8 Authors: Lainie Schuster and Nancy Canavan Anderson Call Number CMT103 |
 |
Good Questions Great Ways to Differentiate Mathematics Instruction Author: Marian Small Call Number CMT116 |
 |
Young Mathematicians at Work: Constructing Multiplication and Division Authors: Catherine Twomey Fosnot and Maarten Dolk Call Number CMT100 |
 |
Uncovering Student Thinking in Mathematics Grades 6-12 Authors: Cheryl M. Rose and Carolyn B. Arline Call Number CMT111 |
 |
Investigations, Tasks, and Rubrics to Teach and Assess Math Grades 1-6 Authors: Pat Lilburn and Alex Ciurak Call Number CMT128 |