At all levels, math problem solving requires specific, ordered steps. Simple recall of steps is only a small part of the process. The desired learning outcome is for students to be able to identify the appropriate procedure and to understand how to apply it and why it works. Students with disabilities and other students who struggle with math may have difficulty remembering, understanding, and/or executing steps in the problem-solving process. The Proceduralizing Strategy (Thomas, Brunsting, & Warrick, 2010), when used throughout Tier 1, 2, and 3 instruction, can reduce barriers with recall and application.
Proceduralizing supports students in mastering recall, comprehension, and application of procedural steps. With the increased rigor and the addition of open-ended questions on the Standards of Learning Assessments in Virginia, skill mastery is crucial to students’ mathematical success. Students with disabilities benefit from instructional approaches, including explicit and systematic instruction, think-alouds (Vaughn, Wanzek, Murray, & Roberts, 2012), and peer coaching (McDuffie, Mastropieri, & Scruggs, 2009). The Proceduralizing Strategy encompasses all of these techniques and could serve as a vehicle to help students with disabilities master certain math skills.
The National Council for Teachers of Mathematics (2000) promotes application of math knowledge using the Process Standards: problem solving, reasoning and proof, communication, connections and representations. Math lessons, therefore, should include opportunities for students to express their understanding using one or more skills related to those standards. The Proceduralizing Strategy addresses the problem solving and communication standards, and teachers can use this flexible strategy to present new information in whole-group instruction in Tier 1 or as specialized instruction to reinforce and remediate in Tiers 2 and 3. For example, teachers can intensify instruction in the upper tiers by chunking and providing written prompts and cues.
The steps for Proceduralizing are noted in Figure 1.
Figure 1. Proceduralizing Strategy steps.
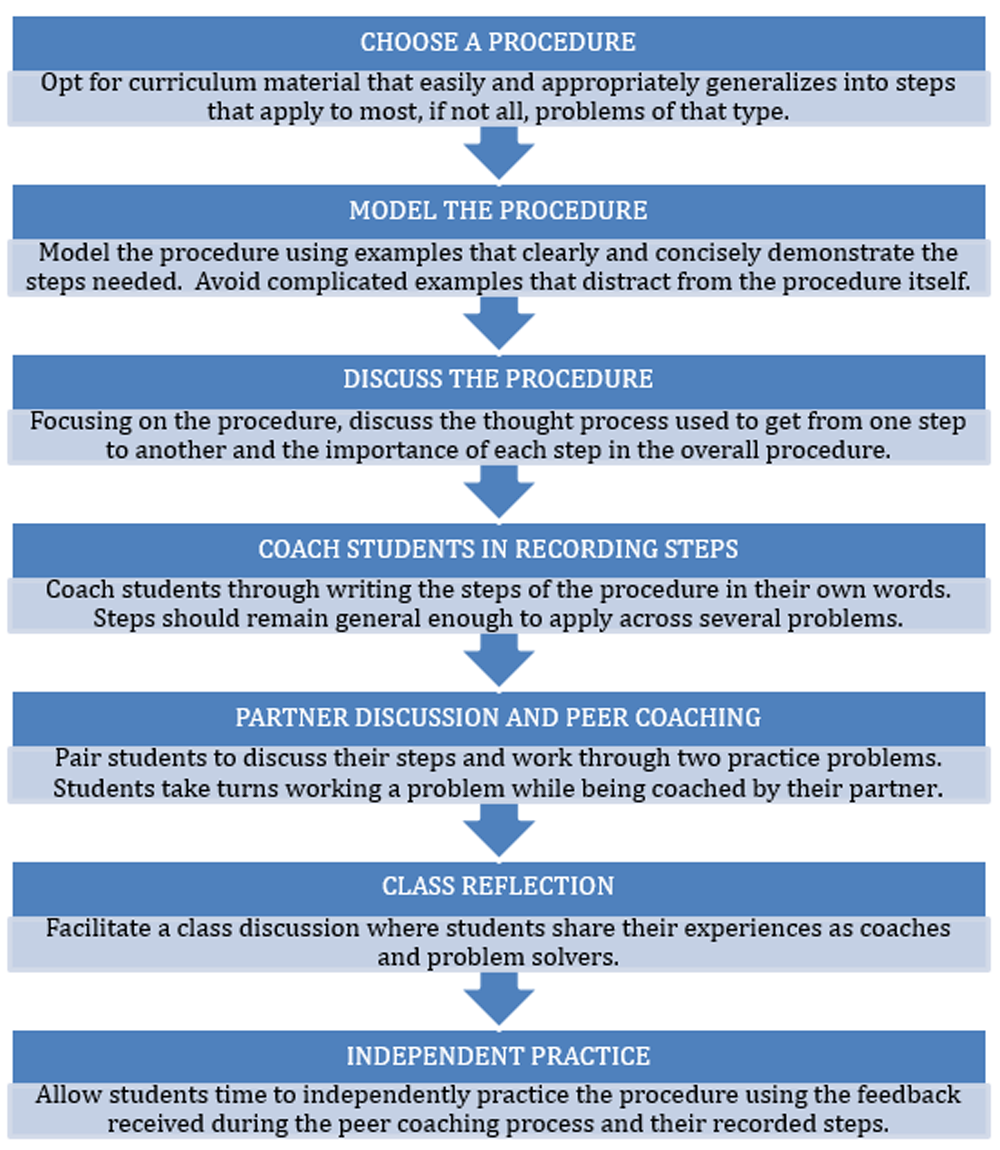 (Adapted from Thomas et al., 2010, pp. 26-27)
(Adapted from Thomas et al., 2010, pp. 26-27)
Classroom Example
The following provides a classroom example showing how the Proceduralizing Strategy may be used to teach students slope and writing linear equations. A similar process may be used for teaching other math strategies as well.
Choose a Procedure
An important procedure in Algebra 1 (VA SOL A.6) is determining the slope between two points and producing the equation of the line. Students need to understand and apply this procedure in Geometry, Algebra 2, and beyond. The Proceduralizing Strategy may be used to create mastery around this skill.
Model the Procedure
Teachers can model the procedure using an example that clearly and concisely demonstrates the steps needed to solve the problem. Avoid complicated examples that contain skills that might distract from the flow of the steps needed to solve a problem (e.g., how to add and subtract fractions, adding and subtracting integers, or denominators of zero). Teach and review any prerequisite skills prior to modeling using exit tickets or class warm-ups to address common student barriers.
Example: Find the slope and equation of the line passing through the points (8, 4) and (5,10). Below is a list of four general steps to be used during the modeling portion of this procedure. Cues are noted in bold.
Step #1: LABEL your points.
One point is (X1, Y1), the second point is (X2, Y2).
Step #2: Find the SLOPE between the two points.
Substitute values into the slope formula.
m = (Y1 – Y2)/(X1 – X2). Now simplify to determine the value of the slope.
Step #3: Solve for b (y-INTERCEPT) of the line.
Write down y = mx + b. Substitute the X1 value for x, the Y1 value for y and the slope value for m. Solve this equation for b.
Step #4: Write the EQUATION for the line between the two points.
Write down y = mx + b. This time, substitute only the slope value for m and b value for b. Leave y and x as variables in your final answer.
Discuss the Procedure
When modeling math strategies, the think-aloud approach is helpful. Saying aloud the thinking that goes into each step of the procedure is beneficial for the student as well as for the teacher. That is, the student is able to hear how to maneuver through a problem using appropriate questions and connections, and the teacher, listening to students problem-solve by thinking aloud, gains a formative evaluation, revealing what the student does and does not understand. Teaching students to softly think aloud as they work provides a method for them to “… stay focused on their work and organize their mathematical thoughts …” (Lee, 2015, p. 285). Students needing explicit instruction on how think-alouds work may be provided with prompts and sentence starters such as the following to help them attack the problem.
- “What is the problem asking me to figure out? I am trying to figure out …”
- “What strategy/formula/equation do I need? The strategy/formula/equation I will use is … because …”
- “What information do I need in order to use that strategy/formula/equation? I need to know …”
- “Do I have all the information I need? If not, how can I get the pieces I am missing? I have … and still need …”
Teachers can model a similar question-and-answer approach each time they present a problem to demonstrate the mental process used in all stages of problem solving.
Coach Students in Writing Steps
The first problem modeled should be followed by a second example, with the teacher continuing to model the procedure using the think-aloud approach to allow students to write each step in their own words. The object is not to have them copy predetermined steps, but to give students the opportunity to internalize and gain ownership and autonomy by writing the steps in their own words and in a manner that holds most meaning to them. The teacher’s role, in turn, is to coach students in recording steps that remain general enough to apply across several problems.
Partner Discussion and Peer Coaching
Once students have recorded their steps, they are grouped in pairs to discuss their steps and work through two practice problems. Groups of three may be provided three practice problems. Problems should be comparable to those modeled during instruction; avoid complex examples that may divert focus from the procedure to mathematical operations that may derail students.
One at a time, students work through a problem without the use of their written steps while their partner coaches them using his or her own written steps as a reference. This opportunity for peer coaching allows students to explain the problem, get immediate feedback, and execute the steps on their own for the first time. By providing student groups with the solutions to their problems, they receive immediate feedback on their execution of the procedure, which supports their accurate application of the process.
Class Reflection
After all students have had an opportunity to work through one practice problem, the teacher facilitates a class discussion in which students share their experiences – both positive and challenging – as coaches and problem solvers. Students then add to or adjust their steps, if needed.
Independent Practice
For independent practice, assign an exit ticket, classwork and/or homework using the procedure on simple problems before progressing to more difficult problems.
Proceduralizing In the Co-Taught Classroom
Co-teachers can use proceduralizing to address varying levels of student needs. Using this strategy within a co-teaching approach allows teachers to monitor how students word their steps, coach their peers, and understand the application of the procedure. Further information on co-teaching approaches may be found in the Co-Teaching Considerations Packet.
Parallel teaching (Tier 1) allows students more opportunities to ask questions of and respond to questions from the teacher or peers. Teachers can use alternative teaching (Tier 2 or 3) when a smaller group needs more intense instruction than can be provided in the whole group. Students in the smaller group practice further with the Proceduralizing Strategy, while the other students, who may not require such a formalized procedure, practice with a less explicit method. Co-teachers could use One Teach, One Observe to collect data to inform future instruction. For instance, one teacher observes students, making note of:
- students having difficulty with writing the steps in their own words;
- student interactions during peer coaching;
- teacher wait time; and
- effectiveness of the think-aloud process.
Further, utilizing the Team Teaching approach with this strategy, one co-teacher could clarify steps or model mental questioning during the problem solving while the other co-teacher answers. The possibilities are endless.
In summary, the Proceduralizing Strategy allows students to learn math content through explicit and systematic instruction, think-alouds, and peer coaching. They then use communication and problem solving to demonstrate their math knowledge. This strategy is packed with effective approaches that support students with disabilities and other students who struggle in math.
References
Lee, J. (2015). “Oh, I just had it in my head”: Promoting mathematical communications in early childhood. Contemporary Issues in Early Childhood, 16(3), 284-287. doi:10.1177/14639491156 00054
McDuffie, K. A., Mastropieri, M., & Scruggs, T. E. (2009). Differential effects of peer tutoring in co-taught and non-co-taught classes: Results for content learning and student-teacher interactions. Exceptional Children, 75(4), 493–510.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Retrieved from http://www.nctm.org/Standards-and-Positions/Principles-and-Standards/Process/
Thomas, E. J., Brunsting, J. R., & Warrick, P. L. (2010). Styles and strategies for teaching high school mathematics: 21 techniques for differentiating instruction and assessment. Thousand Oaks, CA: Corwin.
Vaughn, S., Wanzek, J., Murray, C. S., & Roberts, G. (2012). Intensive interventions for students struggling in reading and mathematics: A practice guide. Portsmouth, NH: RMC Research Corporation, Center on Instruction. Retrieved from http://www.centeroninstruction.org/intensive-interventions-for-students-struggling-in-reading-and-mathematics




